Transmitter Notes

Transmitter Web Page

Discussion

It is generally accepted that QRP transmitting means that the transmitter output power is 5 watts or less. Most of the transmitters I have built were designed for 1.5 watts or less. For me, the lower the output power the greater the thrill when making a contact. I also know some self-proclaimed QRPp masochists who operate flea-power rigs with great pride and determination. The recent interest in the Pixie transceiver is a good example of this "small power equals big fun" philosophy.
For my popcorn 1.5 watt CW transmitters, I normally use a variant of the Ugly Weekender Transmitter designed by Wes Hayward, W7ZOI. This transmitter is quite similar to the design used by Roy Lewellan, W7EL in his Optimized QRP Transceiver article in 1980.

Presented are several transmitter topics; the Chickadee crystal-controlled novelty transmitter, the Ugly Weekender revisited, a QRO HEXFET power amp for 80 meter band CW and a 6M crystal controlled CW transmitter.

Last updated Sept 6, 1999.

Chickadee Transmitter

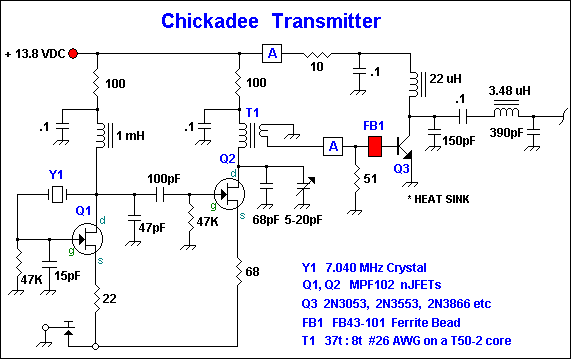
Chickadee Notes

The Chickadee was the first QRP transmitter that I ever used and was designed shortly after I received my amateur radio licence. The original Chickadee consisted of just two nJFET stages and later I decided to "add some power" and the Q3 stage was connected at the points labelled A in the schematic.
The Chickadee is a 40 Meter transmitter and crystal Y1 is a 7.0400 MHz, AT-cut in a HC-6/U metal holder with 30 pF load capacitance. No feedback capacitor(s) were needed across the crystal in the Pierce oscillator as oscillation started every time the key was pressed without them.

The original Chickadee circuit resembles a simple tube transmitter and as shown with a VCC of 13.8 VDC has an output power of 35 - 40 milliwatts. If the VCC is increased to 22 volts or so the output power may increase to 50 - 60 mW. Jeff Damm, WA7MLH suggests AC bypassing the source resistors to ground with 0.01 or 0.1 uF capacitors to get more output power out of the original schematic. More power maybe also achieved by using hotter JFETs such as the J310.
Keying this little transmitter, grounds the source resistors of both Q1 and Q2 and results in very clean transmission with no backwave problems. Admittedly, the keying sounds a little hard, however for a low parts count rig, it is acceptable.

The Q1 1 mH and Q3 22 uH RF chokes are simple epoxy units which resemble resistors. The T1 transformer is wound with 37 primary and 8 secondary turns over the cold end of the primary coil wound on a T50-2 core. XL = 300 ohms and the capacitance needed to resonate this transformer is approximately 76 pF which is easily done with the paralleled 68 pF and 20 pF trimmer caps shown in the schematic.
The original 2 stage Chickadee had no low pass output filter.

Adding the Q3 stage boosts the output power to over 370 mW at a VCC of 13.8 volts. Like the Q2 nJFET stage, Q3 is a simple Class C amplifier. The choice of transistors for Q3 is numerous, however a press-on heat sink is required to protect Q3 from heat damage. The output pi filter as shown is from Doug DeMaw, W1FB and provides both low pass filtering and a 50 ohm impedance transformation. The 3.48 uH inductor can be wound using 27 turns on a T50-2 core using #24 AWG wire. This project is shown chiefly for reference and sentimental reasons and provided much fun on 40 Meters and was used extensively for local code practice in its original 2 stage form.

The Ugly Weekender Revisited

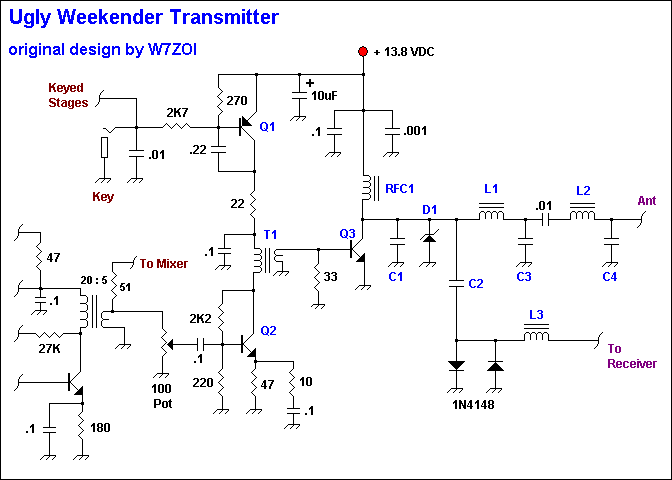
Ugly Weekender Transmitter Revisited Notes

If you need a great low parts-count transmitter for a simple, single band CW transceiver or transmitter it is hard to beat the Ugly Weekender transmitter designed by Wes Hayward, W7ZOI.
The original project is from The Ugly Weekender: parts 1 and 2 , by Roger Hayward, KA7EXM and Wes Hayward, W7ZOI, QST for Aug 1981 and June 1992. The Ugly Weekender articles are mandatory reading for any homebrew radio enthusiast. I have built this transmitter section for 4 different amateur bands ( 160, 80, 40, 30 ) and it has never failed to function perfectly.
Presented will be the necessary data to put this transmitter section on any band that you chose.

Ugly It Is

Some builders have constructed this transmitter using commercially etched, ready-to-go PC boards that have been available for some time. It appears that they have missed the intent of the original article. This transmitter lends itself very well to Ugly Construction and I encourage you to build it as originally planned.

Schematic Explanation

The basic Ugly Weekender transmitter schematic is pretty much intact, however a couple of minor changes have been made and will be discussed. Feel free to use the original design if you prefer.
The schematic above depicts the transmitter section connected to a partial schematic of the VFO buffer/amplifier stage. This VFO design is used in for the Popcorn Superhet projects on this web site.
The keying switch from the original design has been removed from the VFO circuitry and placed in the transmitter section. It maybe preferable to place the transmitter keying switch with the transmitter stages as shown and keep the VFO transmit offset circuit in the shielded VFO box. The keying switch consists of the parts connected to and including Q1. Q1 is a 2N3906, however any general purpose PNP transistor will work as well. The keyed waveform has a smooth rise and fall shape and is clickless.

Q2 can be a 2N3094 or any related NPN transistor such as the 2N2222 or 2N4401. The only major difference from the original schematic on the Q2 stage is the T2 transformer. The original article used two broadband 4:1 transmission line transformers to drive the Q3 stage with a low input impedance. This schematic uses one conventional broadband transformer to achieve the same purpose. This transformer T1, is wound on a FT37-43 ferrite toroid using 12 primary turns and 3 secondary turns distributed evenly over the primary windings. Use number 26 AWG enamel-covered wire. Balun cores such as the BN73-201 are also suitable, although be sure to preserve the 16:1 impedance transformation ratio.

The Q3 stage RF choke RFC1 can be wound using 10 - 12 turns of number 24 AWG enamel covered wire on an FT37-43 ferrite core or as indicated in the original article. The Q3 transistor choices include the 2N3866 or 2N3553 or similar BJT with a heat sink.

QSK and Low Pass Filter Sections

The Q1 and Q2 stages use untuned transformers and are suitable for all of the MF and HF bands. The original Ugly Weekender article had the transmitter on the 40 meter band and it is easily placed on any band of your chosing by changing the design frequency of the output low pass filter and the series-resonant circuit used for QSK transmit/receive switching. Specifically this refers to components C1 to C4 and L1 to L3

Low Pass Filter

The low pass filtering in this transmitter is achieved by connecting two 50 ohm PI filter sections together with a 0.01 uF coupling capacitor. While these sections could be connected together in a tradional half-wave filter fashion and the coupling cap placed before the filter, the method used by W7ZOI leads to easy filter design. The first order of business is to determine what cutoff frequency to use. One easy way to determine the -3dB cutoff frequency is to build a filter around standard value capacitors since you can always wind any needed inductances on powdered iron toroids. The Pi-Filter program offered on this web site makes this exceedingly easy and saves a lot of number crunching. You can chose the cutoff frequency to suit capacitors that you have on hand or by trying to get close to a desired cutoff frequency using standard value capacitors.
The following text refers to the below Pi Filter schematic for clarity however the principles are easily applied to the Ugly Weekender transmitter filter stages:

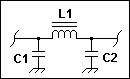
Consider the original low pass filter for 40 meters. Wes Hayward chose a cutoff frequency of 7.40 MHz which means that the individual Pi filter elements are 1.08 uH for the inductor ( L1 ) and 430 pF for each capacitor ( C1 and C2 ). I placed a 100 pF cap in parallel with a 330 pF cap to get the 430 pF capacitance in my version of the 40 meter low pass filter. He could of easily chose a 390 pF capacitor on each side of the filter for a cutoff frequency of 8.18 MHz. How close to the band edge frequency you want to get is up to you. If you want to have an fco just above the higher band limit you will probably have to parallel 2 capacitor values as W7ZOI did. If you are a more frugal builder, you can use the nearest standard value capacitor that will provide an fco above your upper band limit. Using software to determine the filter elements is the most rapid method to do this, but here are the formulas right out of the PI Filter program:

Cutoff Frequency = 1000000.0 / ( Capacitance * 6.283 * 50.0)

The Frequency answer will be in MHz and the Capacitance variable refers to the picofarad value for C1 and C2 which are always the same value ( C1 = C2 ). If you parallel 2 caps for C1 and C2, use the total capacitance value for the Capacitance variable.

Inductance = 50.0 / ( 6.283 * Frequency )

Inductance answer will be in microhenries and the Frequency variable is in MHz.

Lets build a filter for the 30 meter band. The largest standard value that you can use for C1 and C2 is 270 pF, which gives a cutoff frequency of 11.79 MHz. This maybe acceptable to you however perhaps you would like a cutoff closer to the upper band limit of 30 meters. Placing a 33 pF cap in parallel with C1 and C2 would result in a total capacitance of 303 pF and an fco of 10.51 MHz. This would be a great filter. The required inductance to resonate 303 pF at 10.51 MHz is 0.76 uH. Using the CoilBulder program this can be constructed with 14 turns of number 22 AWG enamel covered wire on a T50-6 core.
The above formulas can be used to build filters using standard capacitor values for C1 and C2. The only problem is that you need to start with a capacitance value and substitute the value up or down with standard or paralleled cap values to reach the desired cutoff value. The starting capacitance can be determined with a formula:

Capacitance = 1000000.0 / ( 6.283 * Cutoff Frequency * 50.0 )

Capacitance answer is in pF. Cutoff Frequency is in MHz and is the desired cutoff frequency for your filter.

The starting capacitance formula will get you going and you can use either the program or other formulas to design your filter. Another alternative is variable capacitors and/or inductors, but I will not go there.
Once your filter is designed, all that is left is to design the values for series-resonant T/R components C2 and L3 of the Ugly Weekender Transmitter schematic on this web page.

Transmit / Receive Circuit

The following text now refers to the Ugly Weekender transmitter schematic on this web page.
The Ugly Weekender transmitter featured a clever circuit to provide QSK switching when used as part of a transceiver. The antenna is connected to both the receive input and the transmitter output at all times. While transmitting, the back-to-back diodes in the schematic conduct and prevent the RF level from exceeding 0.7 volts RMS. I have used this scheme with power output levels of over 50 watts using a higher inductance to capacitance ratio to keep the current in the diodes low. The W7ZOI T/R scheme also adds selectivity for the receiver as the antenna input is connected to the receiver through a low pass filter. It is necessary to design a series-resonant circuit to connect the low pass filter to the receiver in order to minimize signal loss on receive. The inductive reactance of the inductor L3 and the capacitive reactance of capacitor C2 are equal at the operating frequency. It seems that using a reactance of ~450 ohms at the lower band edge works well.
To design this circuit, first get the value for C2 by the following formula :

Capacitance = 1000000.0 / ( 6.283 * Lower Band-Edge Frequency * 450.0 )

The Capacitance answer will be in pf and the Lower Band-Edge Frequency is in MHz.

For the 40 meter band this means that C2 is 51 pF. If I only had a 47 ohm capacitor on hand, I could substitute a 47 pF value for C2. This of course means that my XC is no longer 450 ohms and I will need to re-calculate the capacitive reactance as the XC value is also the inductive reactance value ( XC = XL at resonance ) which is needed to calculate the inductor value for L3.

Capacitive Reactance = 1000000.0 / ( 6.283 * Capacitor Value * Lower Band-Edge Frequency )

Capacitive reactance is in ohms, Capacitor Value in pF and Frequency in MHz.

You will need to do this whenever the 450 ohms capacitive reactance value does not not give a standard value capacitor. Simply substitute the nearest standard value or parallel an additional capacitor to get near the value and re-calculate the XC. Use the XC and thus XL value to calculate the needed inductance for inductor L3 using this formula :

Inductance = XL / ( 6.283 * Lower Band-Edge Frequency )

If I used the 47 pF cap for C2, the XC = 484 ohms and the required inductance for L3 = 10.2 uH. In Wes Haywards original article a 51 pF cap was used for C2 and L3 was 10.1 uH and the XC/XL = 446 ohms.

The final variable to be calculated is the new capacitance for C1. When transmitting, C1 and C2 are effectively in parallel and the C2 value must be subtracted from the original Pi filter C1 value. As you recall, the value determined for C1 when doing the PI Filter calculations was 430 pF in Wes Haywards design for 40 meters. Subtracting C2 from C1 = 430 pF - 51 pF = 379 pF. Wes used a 390 pF value for C1, substituting the nearest standard value capacitor.

Lets calculate all the values for a 15 meter band output section using standard value capacitors :
Cutoff Frequency chosen = 21.65 MHz. C1 = 120 pF, C2 = 18 pF, C3 = 147 pF, C4 = 147 pF, L1 = 0.37 uH, L2 = 0.37 uH and L3 = 3.19 uH.
Ideally C1 should have been C3 - C2 or 129 pF , however a 120 pF value was substituted. I believe that it is better to go low with the C1 value as the Zener diode D1 exhibits some capacitance to the circuit as well. For C3 and C4, parallel a 120 pF with a 27 pF capacitor to make the required 147 pF. The inductors are easily wound on powdered iron toroids.

Series-Resonant Variations

A slightly different variation of the series resonant circuit works well on 80 and 40 meters. A RFC of 15 uH is used as the inductor for L3. At 3.5 MHz, this choke has an inductive reactance of ~330 ohms. The capacitance to resonate the circuit ( C2 ) is ~138 pF. Since your choke is generally off by 10% or more it is necessary to tune the C2 value by placing a fixed value cap in parallel with a trimmer cap so that the circuit can be peaked for maximum signal strength to the receiver. The choke value is not critical as Qu is low and bandwidth is high, but tuning is necessary. For a transmitter on 3.5 MHz, I once used a 15 uH RFC for L3 with a 68 PF cap in parallel with a 90 pF trimmer cap for the C2 caps and this combination tuned perfectly. This circuit does not appear to critical with respect to choke selection and the XL and XC values. Experimentation is fun and can be used to suit the parts that you have on hand.

Conclusions

The zener diode D1 is a 33 - 36 volt 400 mW unit and will exhibit some shunt capacitance and may effect the tuning of the low pass filter stages and in turn may reduce the output power somewhat. For a popcorn tranmitter, you need not worry about it too much. Driving the PA for an output power above 1.5 watts may result in some stability problems and is not recommended.
An extensive body of work regarding QRP transmitters has been written by the late Doug DeMaw, W1FB. His QRP NoteBooks and many articles for QST and CQ magazines can provide a wealth of information to aid in the design and building of QRP transmitters. Consult the web page entitled Selected QRP Reading List for more information.

A 3.5 MHz HEXFET RF Power Amplifier

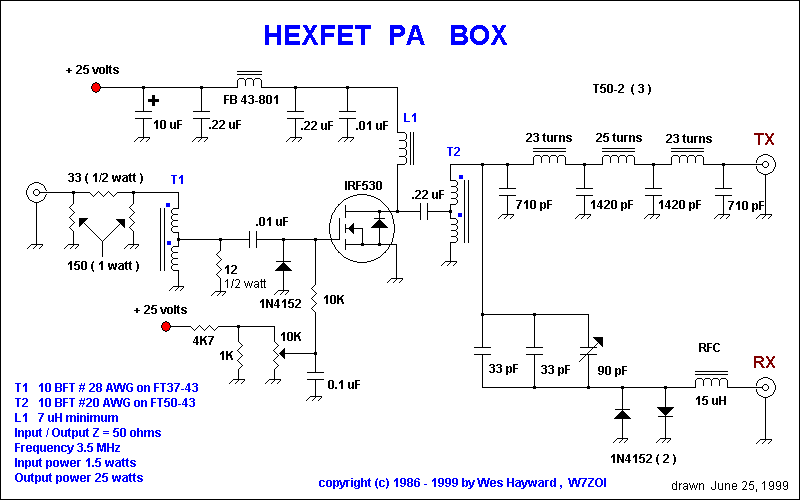
3.5 MHz PA Box For CW

Although , I am a tried and true QRP operator, it is nice to run QRO at times when the band conditions are poor on 80 and 160 meters. A few years ago, I asked Wes Hayward about using a HEXFET to make a brick for 80 meters and he gave me the above schematic. I built the project and it worked very well. I worked many stations on the east coast and even worked an Italian station using a folded Marconi antenna in the mountains while on a camping trip. Unfortunately, while on the camping trip, the rig was run over by the truck and camper and had to be given a decent burial.
This brick was excited with a VFO controlled version of the Ugly Weekender which had an output power of 1.5 watts. I could hook up the brick and run QRO or just use the QRP transmitter to suit the band and battery conditions at the time. We generally placed two deep cycle marine batteries in series to run this amplifier when camping.

Wes Hayward published an article as QST Technical Correspondence in November 1989, pages 38 - 40. This article should be in the library of anyone choosing to use HEXFETS as a transmitter PA. The T/R scheme is described above in the Transmit/Receive Circuit notes. Many thanks to Wes Hayward, W7ZOI for allowing me to display this schematic.

A Six Meter Band Transmitter by VE7GC

VE7GC 50 MHz Transmitter for CW

Here is a 6M CW transmitter by Dick Pattinson, VE7GC which has some great design ideas. The third-overtone crystal oscillator is doubled and finally boosted up in power by a V10K. Feel free to substitute different transistors for Q1 to Q4. Substantially more power is possible with different crystals and operating voltages. A picture of the prototype transmitter is shown below the main schematic. A large black Marconi crystal is on the extreme left , while the output is on the right hand side. Many thanks to VE7GC for the schematic.

Return to the QRP HomeBuilder Homepage